本攻略由【幻月府】月光 制作，不代表官方观点，请以游戏为准

写在前面：

       数字恐惧症患者慎入……看一半受不了可以叉掉……本文更多的是作为学术研究和同好讨论，不接受看不懂无脑喷。关于文章的实用性，仁者见仁智者见智。

       很久之前就想写这样一篇攻略，但碍于一个小问题没有解开，迟迟进展不下去。现在这个困扰多时的问题终于解开了，我们来深度聊聊诛仙手游的宠物系统吧。

       为什么想谈谈宠物系统？因为这是整个游戏里非常非常重要的一个系统！宝宝的作用不用我说了吧，有没有一只适合自己的宝宝，将直接影响到你PK的战局。

       我将从两个大方面来完成本文——

       第一，剖析宠物面板的各项属性，从数据角度研究它们之间的关系；

       第二，宠物技能和面板数据相结合，教你怎样培养一只适合自己的宝宝。

一、宠物面板剖析

       宠物界面包含以下重要属性——成长率、资质、星等、星等百分比、自身技能点数、额外技能点数、亲密度、面板属性。以下所有数据都是建立在常规宝宝基础上的（即黄鸟这个阶层的宝宝），我们不讨论低级宝宝（比如灵猴），也不讨论饕餮这种高级宝宝。

下面逐项说——

【成长率】满值是9.09。成长率影响面板属性，越高则面板属性越高。

【资质】主资质满值是2727，副资质满值是1909，其他两项资质满值是1227。资质同样影响对应属性的面板，越高则面板属性越高。

【星等】未飞升满星15星。飞升满星18星。9星改变宠物外观。

【星等百分比】星等界面括号里的百分比是个很有意思的数据。百分比带给我们两个信息——

1、当前星等百分比数据是升到当前星等的属性加成值，这个属性加成全部是在最基础的属性上计算的。可以认定为是0星，虽然没有0星宝宝。（举个栗子：12星宝宝百分比数据是31.72%，意思是这个宝宝在0星时的属性，增加31.72%，就是它到12星时的属性值。反过来讲，已知一个12星宝宝的属性面板，除以1.3172就是这一项属性的最基础数值，用这个最基础数值乘以1+不同星等百分比就可以计算出你想要的星等属性。）

2、这个百分比还是额外属性加点倍数。（举个栗子：12星宝宝百分比数据是31.72%，你有一个12星宝宝，你要给这个宝宝分配1000点斗志加点，那么1000点生成的属性增长值为1000*1.3172=1317点。这个1.3172就是倍数。）下文有验证。

【自身技能点数】1级宝宝自带5个点数，以后每升一级，增加5个点数。飞160宝宝，有1255点自身点数。

【额外技能点数】花费非绑定元宝购买的点数。2元宝/点。可购买点数随着宝宝等级的增加而增加，但不是每级恒定。

59级的时候，共有40点额外点数；

59—68级，每升一级，给4点额外点数；

69—78级，每升一级，给5点额外点数；

79—88级，每升一级，给6点额外点数；

以后每10级点数增涨1点，89级开始是7点，99级开始是8点，以此类推，增涨到148级的时候，给12点。

149—飞67级，每升一级，给13点额外点数；

飞68—飞77级，每升一级，给14点额外点数；

飞78—飞87级，每升一级，给15点额外点数；

以后每10级点数增涨1点，到18点封顶不再增加。从飞108级开始，后面的点数都是18点。

飞160宝宝，有2446额外可购买点数，总共需要4892非绑定元宝。

自身技能点+额外购买点=1255+2446=3701。这个值，在传承界面可以看到。

【亲密度】影响技能的释放率，满亲密释放率50%。

【面板属性】这是本文重点要研究的，面板属性是技能计算的根值。面板属性受上面多种属性的直接影响。

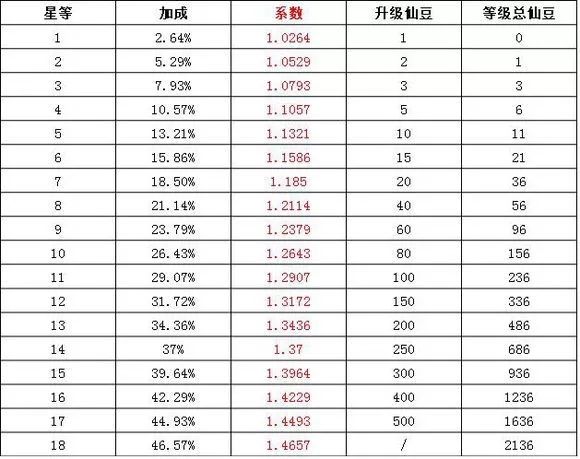
上面这个图是不同星等对应的百分数，以及不同星等升级需要的仙豆数。

二、星等百分比

       我们先验证上文说的星等百分比即为加点倍数这个说法，因为后面会用到这个结论。这个很重要！（看下图）

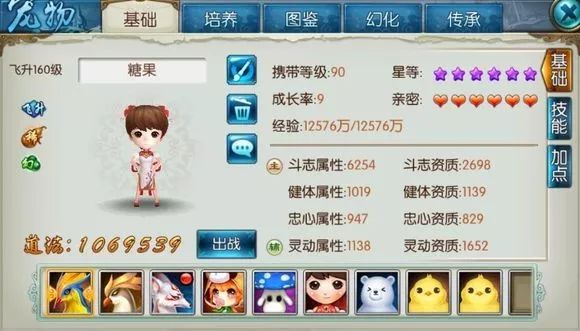
       上面第一张图，是买满点数的宝宝，并且点数全加到斗志的属性图，可以看出斗志属性为6254。

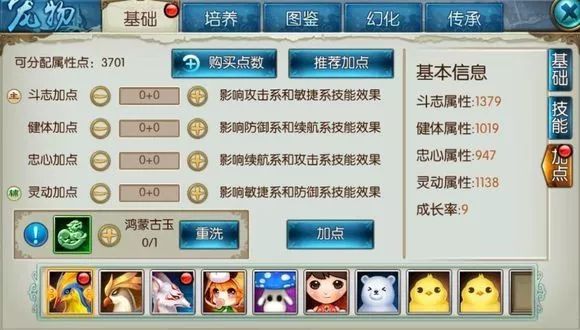
       第二张图，我把点数洗掉，斗志属性变成了1379。

       6254-1379=4875。也就是说3701的满点数给斗志属性增加了4875这个值。

       每一个点数的增加值为：4875/3701=1.317211564442043≈1.3172。

       对照开文时的图表，31.72%刚好是12星宝宝的百分比。

       所以结论就是：星等百分比是额外属性加点倍数。

       PS：可能有人会反驳我只用12星宝宝做了测试，样本太少没有参考性。其实这个值在实际的求证过程中我分析了大量的数据，但结果一直跟猜想有出入，直到一次偶然的求证中，我发现了百分比这个直接的系数就是加点倍数。之前我用18星宝宝和17星宝宝都做过测试，所以这个值不用怀疑，是准确的。比如18星宝宝的系数为1.4657，即3701点数会带来3701*1.4657=5425的属性增涨。

三、极值

       有了上面的铺垫，我们来看看属性和成长率以及资质之间的关系。

       在研究之前，必须要确定几个极值，这是一个封顶和框架。

       我们知道，成长率满值9.09，主资质满值2727，副资质满值1909，其他资质满值1227。那么如果这些指标全满，不加点的属性面板是怎样的呢？

       上面这只稀有雪宝，副属性1340，非主副1165。我对比了很多只雪宝，都是这个值。

       主属性的初始值我们用上文的结论来求一下。

       看上图，这只雪宝明显分配了斗灵点数，而健忠是没有加点的。灵动的初始值跟健体的相同，为1165，灵动增长值为：4029-1165=2864。

       根据18星系数，灵动被分配点数为：2864/1.4657=1954。

       分配给斗志的点数为：3701-1954=1747。

       所以斗志的初始值为：4111-1747*1.4657=1550。

       结论：飞160满18星宝宝，成长率以及四项资质全满——主属性为1550，副属性为1340，非主副属性为1165。（敲黑板，划重点！）

       PS：实际查看主属性最简单的办法就是让雪宝的主人把加点全洗掉，就能看到一个直观的数据，但是因为这个宝宝不是我的，没办法要求人家洗点。而我在求证这个1550数值的时候，由于当时还没有发现星等百分比系数，用了一种更为复杂的方法。那种方式过于繁琐，这里就不说了，但是也变相验证了1550这个值的准确性。

四、属性和成长率以及资质的关系

       这是本文的重点，也是我开文时提到的一直困扰我解不开的难题。（现在解开了）。

       我们知道，成长率越高，肯定属性值就越高，也知道资质越高，属性值也越高。但是在成长率和属性坐标系，或者资质和属性坐标系中，那个关系图一定不是线性的，而是一条曲线。因为诛仙很多的两相制约的属性关系图都是曲线，比如暴伤暴减差值所影响的暴击伤害倍数就是曲线。这条曲线的特点是随着x的增大，y的增涨速度衰减，曲线终端最终近乎平行于x轴。给你们直观的图感受下。

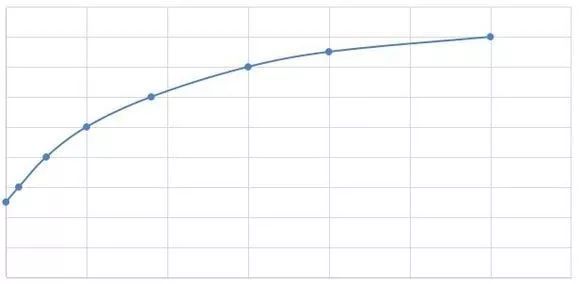
       宠物属性受成长率和资质的双重影响关系图我认为也是曲线，但是因为两个值同时左右着属性的变化，并不是简单的x和y的关系。

       之前我在对比了多组数据后，有一些猜想——

       猜想1：成长率和资质在实际情况下都和极值有一个占比，这个占比是不是同样影响了属性的占比呢？最终研究下来失败了，跟占比没有关系，而恰恰通过占比求出来的属性值跟实际值跳跃性很大。所以这个不成立。

       猜想2：资质和成长率是不是影响宠物每升1级自然增涨的属性值呢？研究下来发现，这个确实是有影响的，低资质和低成长的时候，宠物每升1级有的时候属性增涨1点或是2点，高资质和高成长的时候，有时增涨4点或者5点。但是这个增长值和资质成长的公式，也不能确定。逐级研究又失败了。

       猜想3：从阶段性的属性增涨速率入手，看下不同阶段的速率是不是能构成一条可求方程的曲线。这个过程数据量巨大，需要研究多组数据的差值求出和每1单位成长资质的比值。研究下来，这条曲线并不规则，还是失败了。

       上面的种种猜想都是考虑了成长率和资质对于属性的双重影响。简单说，就是比如成长率恒定，求出一个资质对于属性的增幅，而当成长率变化，来研究这个增幅是怎样变化的。这很困难，研究了很多数据，我求不出，这也是上文提到的一直困扰我的难题。于是我把成长率和资质两者分开来，这个难题终于解开了。

五、恒定成长下的属性研究

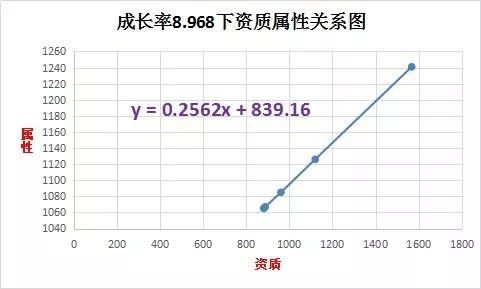
       看上面这三张图，前两张图捕捉了两只成长率都是8.968的熊孩子，提取两只宝宝没有加点的属性和资质数据五组。（881，1065） （888，1067） （961，1085） （1120，1126） （1568，1241）。

       以资质为x值，属性为y值生成散点图，比较意外的是，属性成长趋势居然是近似线性的。对8.968成长率下的散点进行线性拟合，方程为：y=0.2562x+839.16。

       把第一张图中的斗志资质2643代入方程，得到未加点斗志属性为1516。

       图一中斗志分配和额外点数3701点，根据上文讲到的，18星宝宝3701点数生成3701*1.4657=5425属性值。

       1516+5425=6941，刚好和图一中的斗志属性6942是吻合的，说明在恒定成长率下，资质对属性的影响确实是近似线性的关系。

六、恒定成长资质属性公式

       上文计算的线性公式是在18星的基础上进行的，而很多时候，我们的宝宝形态多种多样，星等不一，资质不一，成长率不一，那么对于不同数据的宝宝，有没有一个通用的恒定成长公式求证方法呢？我用我自己的宝宝做下测试。

       PS：请注意，我这里说的是公式的求证方法，并不是求一个通用的公式。意思就是告诉大家怎么求一个适合自己宝宝的公式。每一条公式对应一种宝宝数据，因为宝宝不同，所以每一条公式也都不会相同。

       我的宝宝数据：星等12星；成长率9；

       资质和属性关系四组：（829，947） （1139，1019） （1652，1138） （2698，1379）

       这里我用直线的两点式公式来求这条方程式，之所以可以用两点式，是因为上文验证了这个资质属性关系是近似线性的。但是请注意，这里我用的近似线性这个说法，因为样本散点太少，所以实际上这不是一条绝对的直线，而用更少的两点求出来的方程绝对存在误差，点数用的越少，误差越大。

但是没办法，如果不采用两点式，一般玩家不容易求出属于自己的方程。

       普及一下高中数学直线的两点式方程：一条直线上存在两个点P1（x1，y1），P2（x2，y2），两点确定的直线方程为（y-y1）/（y2-y1）=（x-x1）/（x2-x1）。

我取（829，947）和（1139，1019）这两个点，求出方程为：y=0.2323x+754.46。

代入1652和2698两个值验证，结果为1138和1381，与实际结果1138和1379误差很小。所以可以确定，这条方程就是适合我这只宝宝的方程。

按照上述两点式的方法，任选两个点，你们可以求出适合自己宝宝的方程。这条方程适用于你的星等，成长和不同资质，独一无二且准确。

       PS：但是请特别注意，以上所有数据都是建立在宝宝飞160满级状态下。这并不是说非满级求不出方程，而是非满级求出的方程没有用！我们求这条方程式是为了能计算后续很多数据准备的。简单说，你可以利用两点式求出一个宝宝飞117级，12星时的数据，但是你想知道这个宝宝到了18星变成什么样子，这条方程就不适用了，因为到了18星，宝宝等级不可能还是飞117级。所以，求方程，都是建立在宝宝满级基础上。

       那么宝宝满级时这条属于自己的公式能干什么呢？

       得出这条公式是很容易的，只用了两个点。有了这条公式，你能求出当前宝宝在后续进化形态后的数据。

       最重要的是，这条方程给后续求成长资质对属性的双重影响公式提供了准备。

七、恒定资质下的成长研究

       捕捉了6只满级18星成长率不同的宝宝，数据量比较大，这里就不截图了。

       首先，利用上文提到的两点式公式，分别求出属于每只宝宝的方程。即六条不同成长率下的资质属性关系方程。

       我随机选取一个数值作为固定的资质，代入每一条方程求出属性。这里我选取888这个资质数值，分别代入每一条方程，求出六个属性值。意思就是，当资质恒定为888时，不同的六个成长率，对应六个属性值。

       这时资质恒定，我们用成长率作为x值，属性为y值，生成六个散点。画出图来发现，在固定资质下，成长率对属性的影响也是近似线性的。看下图。

八、恒定资质成长属性公式

       上文提到资质恒定，成长率对于属性的影响也是近似线性的。怎么求这条线性公式呢？

       首先利用第五条中讲到的，先求出一条属于自己宝宝的成长恒定下的资质属性关系公式。然后，去本服或者长生界的宝宝排行榜中，捕捉一只满级的跟自己宝宝相同星等的宝宝，求出这第二只宝宝的成长恒定下的资质属性关系公式。现在我们拥有了两条方程式，随机选取一个资质数值，代入到两条方程式中，会得到两个属性值。利用这两个属性值作为y1和y2值，它们对应的成长率作为x1和x2值，就可以用两点式求出当前星等资质恒定下的成长属性关系公式了。

下面举例说明：

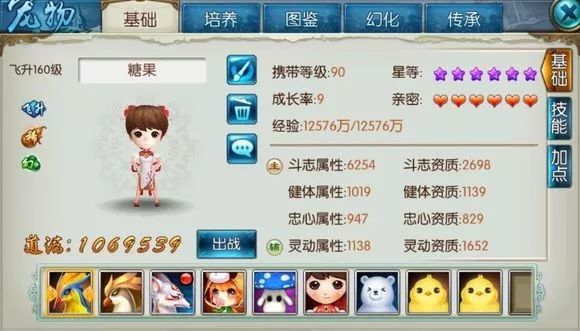
       看上面这两张图，首先要确保两只宝宝都为满级，并且星等相同。

利用两点式求出第一只宝宝在成长率为9时的资质属性关系公式为：y=0.2323x+754.46；

利用两点式求出第二只宝宝在成长率为8.895时的资质属性关系公式为：y=0.2302x+747.49。

我们取值829这个资质。

第一张图中，资质为829的前提下，成长率为9，属性为947；

第二张图中，把829代入第二个公式，得出，成长率为8.895，属性为938。

这时我们得到恒定资质829下的两个点（8.895,938） （9,947），利用这两个点求出成长属性关系方程：y=85.714x+175.57。

       这条方程能干什么呢？

       如果单看这一条方程，意义其实不大。这条方程的最主要作用就是证明了成长对属性的影响也是线性关系的，这很重要，这个线性关系是后面求双重关系公式的基础。后续也会把成长属性关系和资质属性关系做一个对比。

九、成长和资质对属性的双重影响公式

有了上面的基础，就可以求这最重要的一条公式了。

我们借用上面已经求好的公式——

成长率为9时的资质属性关系公式为：y=0.2323x+754.46；

成长率为8.895时的资质属性关系公式为：y=0.2302x+747.49。

令资质为a，代入上面两个公式，得到的值分别为0.2323a+754.46和0.2302a+747.49。

所以，当资质为a时，得到两个点（8.895，0.2302a+747.49）和（9，0.2323a+754.46），利用两点式，求出成长属性关系公式为：

12星：y=(0.02a+66.38)x+0.0523a+157

PS：上面的公式，必须跟着星等走，并且需要宝宝满级飞160。不同星等对应的公式是不一样的。另外，公式具有误差，因为前面提到了，近似线性的图用两点式求出的公式是肯定存在误差的，而这里，两点式利用了两次，所以误差范围会更明显些，但是一般跟实际不会相差5点。

这条公式，对于宝宝的洗点，具有方向性的指导意义。

举例来说，比如我这只宝宝12星，成长率9，忠心资质829，忠心属性947。先计算出12星宝宝的忠心属性（非主副）极值为：1165/1.4493*1.2907=1038。如果想要忠心属性达到1000，那么根据公式就可以计算出多种组合——

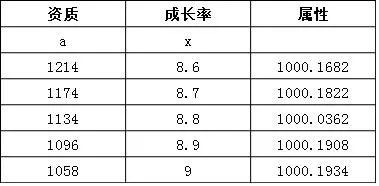
       给大家一些现成的公式，这些公式不是用两点式求出来的，而是我用多点进行的线性拟合，误差非常小，基本上都是小于1点的误差。对比自己的宝宝或者别人的宝宝面板直接用或者验证都可以。注意宝宝需要满级飞160。

       飞160宝宝，令成长率为x，资质为a，最终对应属性为y（注意这里的y是没有加点的属性，具体加多少点按照开文的点数和百分比倍数去算），公式为——

       PS：上面的公式是我用自己捕捉到的数据计算的结果，如果你们自己去捕捉不同的样本去计算，最终的公式每个人都是不一样的，但是，求出的结果y值都会是近乎相同的。拟合的点数越多，公式越精确。

       另外，有的公式x前的系数含有a值，有的却没有，这也是样本不同造成的结果。计算的时候我都是用实际捕捉的宝宝跟计算出的极值雪宝作为数据组，期间发现，当捕捉的宝宝成长率在8.7左右浮动时，实际宝宝拟合公式跟极值拟合公式的斜率是一样的，这样求出来的最终公式x前的系数就不含a。但是含不含a都没有影响，上面的这些公式我已经最大限度地降低了误差。

成长率和资质哪个更重要？

       我记得刚开始接触这款游戏的时候，经常有玩家问，宝宝洗点的时候成长率和资质哪个重要，回答也是二者不一。现在给你们一个数据上的准确结论。

首先要强调的是，成长率和资质共同左右着最终的面板属性，两者同样重要。

如果作为学术研究，非要分出主次的话，结论是：成长率更重要。

       我们用上面讲到的东西验证——

验证1：

12星飞160宝宝，成长率9资质属性关系公式为：y=0.2323x+754.46；

12星飞160宝宝，资质888成长属性关系公式为：y=85.714x+175.57。

第一条公式中，x代表资质，当资质为0时，属性y值为754.46；

第二条公式中，x代表成长率，当成长率为0时，属性y值为175.57。

两个值说明，去掉资质保留成长，属性值依然能保持较高；而去掉成长保留资质，属性值就要低的多了。

但是上面的验证，是在成长率为9，资质为888下的验证，成长接近满值占了便宜，可能不具备代表性，我们来看验证2。

验证2：

12星，成长资质对属性双重影响公式：y=(0.02a+66.38)x+0.0523a+157。

①令a=0，x=9.09，y值为760

②令a=2727，x=0，y值为300

对比760和300这两个值，很容易看出，当去掉资质而成长率为满值，比去掉成长而资质为满值时的属性要高了一倍多。

       综上，成长率更重要。借此也反驳一下早期说资质更重要的观点，为什么早期玩家会有错觉，认为资质更重要呢？因为那时候的数据样本都是级数很低的宝宝，那时的宝宝都没有飞升，随便对比了两只70级的宝宝就说属性相差不大，或者说资质，成长相差怎样云云是很可笑的。举个不恰当的例子，当宝宝级数变成1000级的时候，再抓取两只宝宝，就比你70级的时候直观的多了。